选择排序（Python）

选择排序

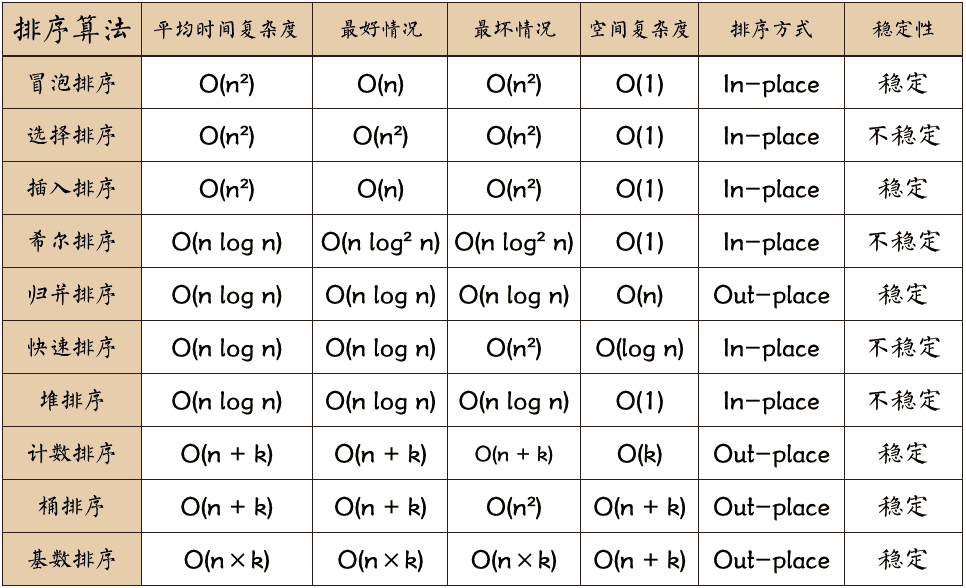
排序算法	平均时间复杂度	空间复杂度	稳定性
冒泡排序	\(O(n^2)\)	\(O(1)\)	稳定
选择排序	\(O(n^2)\)	\(O(1)\)	不稳定
插入排序	\(O(n^2)\)	\(O(1)\)	稳定
希尔排序	\(O(n\log^2 n)\)	\(O(1)\)	不稳定
归并排序	\(O(n\log^2 n)\)	\(O(n)\)	稳定
快速排序	\(O(n\log n)\)	\(O(\log n)\)	不稳定
堆排序	\(O(n\log n)\)	\(O(1)\)	不稳定
计数排序	\(O(n+k)\)	\(O(k)\)	稳定
基数排序	\(O(n\times k)\)		稳定
桶排序	\(O(n)\)	$O(m)$	稳定

算法思路

从待排序数列中选择最小的元素，将它与数列的第一个元素交换位置。再从数列剩下的元素中选择出最小的元素，将它与数组的第二个元素交换位置。不断进行这样的操作，直到将整个数组排序。

算法实现

设置标志位记录待排序数列中最小元素的下标，每次遍历完成后都将最小元素放在已排序数列的末尾。

def selection_sort(arr):
    arr_len = len(arr)
    if arr_len < 2:
        return

    for i in range(arr_len):
        min_index = i
        for j in range(i+1, arr_len):
            if arr[min_index] > arr[j]:
                min_index = j
        if i != min_index:
            arr[i], arr[min_index] = arr[min_index], arr[i]

---

本博客文章仅供博主学习交流，博主才疏学浅，语言表达能力有限，对知识的理解、编写代码能力都有很多不足，希望各路大神多多包涵，多加指点。