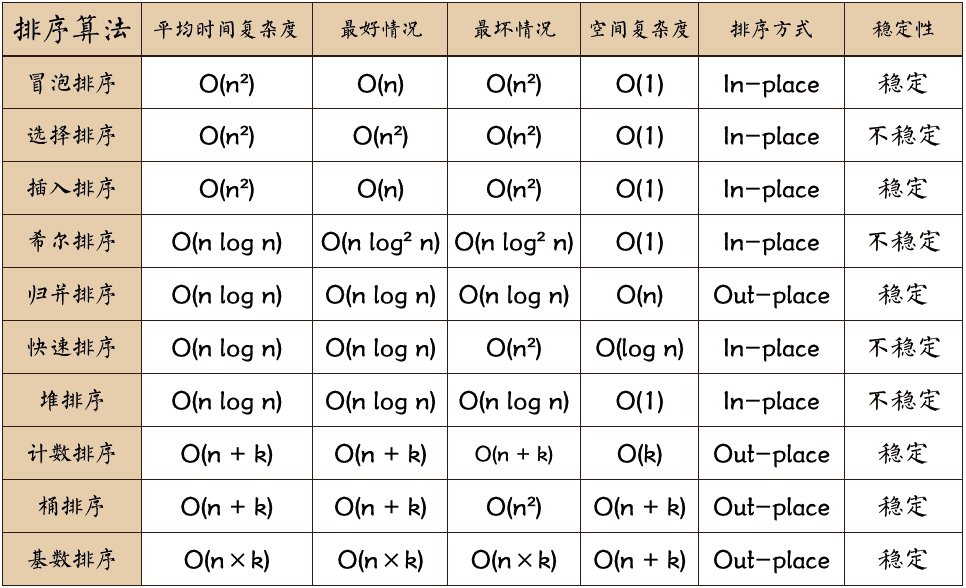
堆排序
| 排序算法 | 平均时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 冒泡排序 | $O(n^2)$ | $O(1)$ | 稳定 |
| 选择排序 | $O(n^2)$ | $O(1)$ | 不稳定 |
| 插入排序 | $O(n^2)$ | $O(1)$ | 稳定 |
| 希尔排序 | $O(n\log^2 n)$ | $O(1)$ | 不稳定 |
| 归并排序 | $O(n\log^2 n)$ | $O(n)$ | 稳定 |
| 快速排序 | $O(n\log n)$ | $O(\log n)$ | 不稳定 |
| 堆排序 | $O(n\log n)$ | $O(1)$ | 不稳定 |
| 计数排序 | $O(n+k)$ | $O(k)$ | 稳定 |
| 基数排序 | $O(n\times k)$ | 稳定 | |
| 桶排序 | $O(n)$ | $O(m)$ | 稳定 |
堆排序使用一种被称为堆的数据结构进行排序。
堆
（二叉）堆是一个数组，它可以被看成一个近似的完全二叉树。树上的每一个结点对应数组中的一个元素。除了最底层外，该树是完全充满的，而且从左向右填充。二叉堆可以分为两种形式：大顶堆和小顶堆
大顶堆：每个结点的值都大于或等于其左右孩子结点的值，堆中最大的元素存放在根节点。
小顶堆：每个结点的值都小于或等于其左右孩子结点的值，堆中最小的元素存放在根节点。
由于堆是一个数组，对于大顶堆它的实际存储为：
给定堆中的一结点下标为 ｉ，则其左孩子和右孩子对应下标分别为 2ｉ+1 和 2ｉ+２，若数组下标自 1 开始，则其左孩子和右孩子对应下标分别为 2ｉ 和 2ｉ+1。
堆排序算法（以大顶堆为例）
将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余 n-1 个元素重新构造成一个堆，这样会得到 n 个元素的次小值。如此反复执行，便能得到一个有序序列了
维护堆性质的函数
整个排序算法都建立在待排序列为大顶堆的基础上，而在根结点与末尾元素进行交换时会破坏大顶堆结构，需要有对大顶堆进行维护的函数。
在该函数中给出根节点下标 root，根据堆的性质得到其左右孩子结点下标，选出三个结点的最大值，并将最大值下标赋给 max。若 root 为最大结点，以 root 为根节点的子树已经是最大堆，程序结束。否则，最大值是 root 的某个孩子结点，交换 max 结点同 root 结点的值。由于 root 结点的一个孩子结点值发生改变，以该孩子结点为根的子树可能违反最大堆性质，递归调用函数。
def max_heapify(arr, root):
max_, left, right = root, 2 * root + 1, 2 * root + 2
# 全局变量 arr_len
if left < arr_len and arr[left] > arr[max_]:
max_ = left
if right < arr_len and arr[right] > arr[max_]:
max_ = right
if max_ != root:
arr[root], arr[max_] = arr[max_], arr[root]
max_heapify(arr, max_)
建堆函数
想要进行堆排序，首先需要将初始序列变成大顶堆 我们可以用自底向上的方法利用函数 max_heapify() 将一个初始序列变成大顶堆
def build_max_heap(arr):
# 叶子节点无需维护堆性质
# 不需遍历整个数组
for i in range(len(arr) // 2,-1,-1):
max_heapify(arr,i)
排序函数
将大顶堆根节点与末尾元素进行交换，此时末尾就为最大值。然后将剩余 n-1 个元素重新构造成一个堆，这样会得到 n 个元素的次小值。如此反复执行，便能得到一个有序序列了
def heap_sort(arr):
global arr_len
arr_len = len(arr)
if arr_len < 2:
return arr
build_max_heap(arr)
for i in range(len(arr) - 1, 0, -1):
arr[0], arr[i] = arr[i], arr[0]
arr_len -= 1
max_heapify(arr, 0)
知识来源
«算法导论»第6章堆排序 图片直接从这位大大这拿图并参考https://www.cnblogs.com/chengxiao/p/6129630.html *** 本博客文章仅供博主学习交流，博主才疏学浅，语言表达能力有限，对知识的理解、编写代码能力都有很多不足，希望各路大神多多包涵，多加指点。
