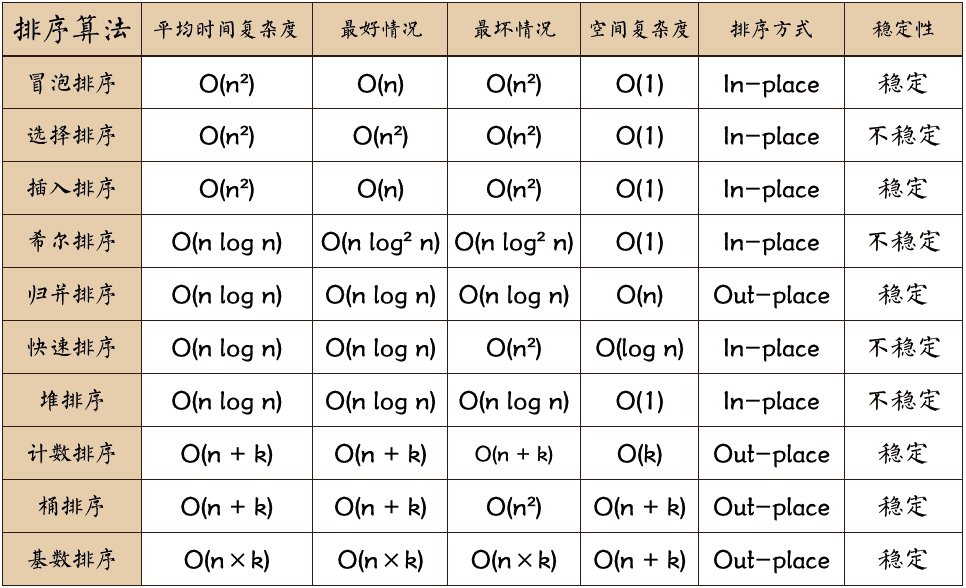
线性时间的排序算法
| 排序算法 | 平均时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 冒泡排序 | $O(n^2)$ | $O(1)$ | 稳定 |
| 选择排序 | $O(n^2)$ | $O(1)$ | 不稳定 |
| 插入排序 | $O(n^2)$ | $O(1)$ | 稳定 |
| 希尔排序 | $O(n\log^2 n)$ | $O(1)$ | 不稳定 |
| 归并排序 | $O(n\log^2 n)$ | $O(n)$ | 稳定 |
| 快速排序 | $O(n\log n)$ | $O(\log n)$ | 不稳定 |
| 堆排序 | $O(n\log n)$ | $O(1)$ | 不稳定 |
| 计数排序 | $O(n+k)$ | $O(k)$ | 稳定 |
| 基数排序 | $O(n\times k)$ | 稳定 | |
| 桶排序 | $O(n)$ | $O(m)$ | 稳定 |
计数排序
计数排序是一种非比较型整数排序算法。计数排序会假设待排序数列中的每个元素都是在 0 到 k 区间内的一个整数,k 不宜过大。
算法思路
对于一个待排序数列中的任一元素 x,统计数列中小于等于 x 的元素个数 i,那么在排序完成的数列,元素 x 就该位于索引 i 处。
算法实现
接收待排序数列 arr 以及数列中的最大值 max ,初始化一个长度大于 max 的数组 temp,初值为零。遍历 arr,将 temp 中以 arr 元素值为下标的元素值 +1,以此计算相同数字个数。
def counting_sort(arr):
max_value = max(arr)
count_len = max_value + 1
count = [0] * count_len
for i in arr:
count[i] += 1
for i in range(1, count_len):
count[i] += count[i-1]
arr_len = len(arr)
result = [0] * (arr_len + 1)
for i in range(arr_len-1, -1, -1):
result[count[arr[i]]] = arr[i]
count[arr[i]] -= 1
return result[1:]
基数排序
算法思路
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。
算法实现
def radix_sort(arr):
max_value = max(arr)
max_digit = 0
while max_value > 0:
max_value //= 10
max_digit += 1
for digit in range(max_digit):
count = [[] for i in range(10)]
for i in arr:
p = i // 10**digit % 10
count[p].append(i)
temp = []
for bucket in count:
for i in bucket:
temp.append(i)
arr = temp
return arr
桶排序
桶排序会假设输入数据服从均匀分布。
算法思路
桶排序会根据待排序数列中所包含的元素值的范围划分多个区间,每个区间称为“桶”,序列中属于相应区间的元素会分到区间相对应的桶中,对每个桶中的元素分别进行排序,再将所有桶中排序后的元素合并在一起,完成整个数列的排序。
算法实现
def bucket_sort(arr, bucket_num=10):
bucket = [[] for _ in range(bucket_num)]
min_, max_ = min(arr), max(arr)
# 划分区间
bucket_size = (max_ - min_) // bucket_num + 1
for i in arr:
p = (i - min_) // bucket_size
bucket[p].append(i)
# 使用插入排序对桶中元素进行排序
for i in range(bucket_num):
insertion_sort(bucket[i])
return sum(bucket, [])
知识来源
«算法导论»第8章 *** 本博客文章仅供博主学习交流,博主才疏学浅,语言表达能力有限,对知识的理解、编写代码能力都有很多不足,希望各路大神多多包涵,多加指点。