冒泡排序

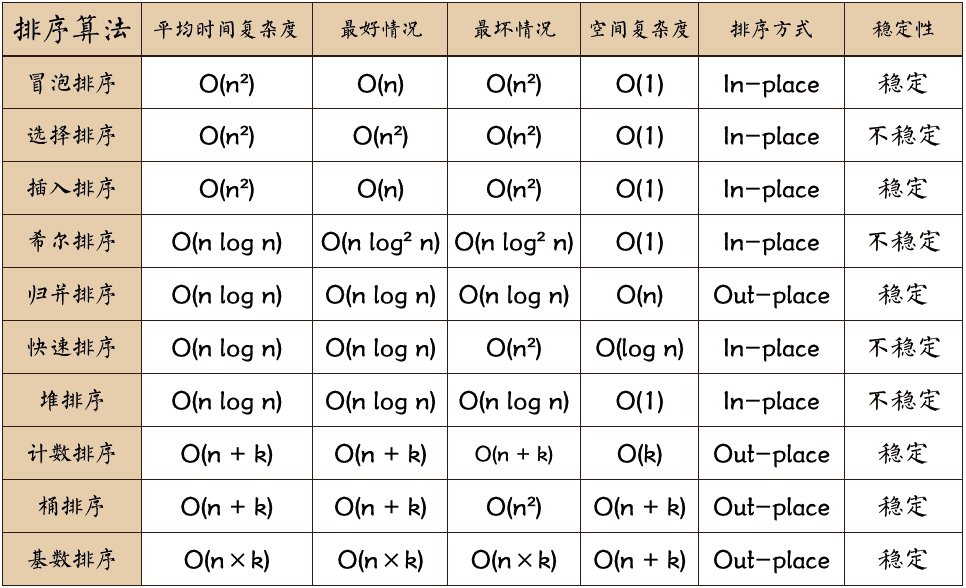
排序算法	平均时间复杂度	空间复杂度	稳定性
冒泡排序	$O(n^2)$	$O(1)$	稳定
选择排序	$O(n^2)$	$O(1)$	不稳定
插入排序	$O(n^2)$	$O(1)$	稳定
希尔排序	$O(n\log^2 n)$	$O(1)$	不稳定
归并排序	$O(n\log^2 n)$	$O(n)$	稳定
快速排序	$O(n\log n)$	$O(\log n)$	不稳定
堆排序	$O(n\log n)$	$O(1)$	不稳定
计数排序	$O(n+k)$	$O(k)$	稳定
基数排序	$O(n\times k)$		稳定
桶排序	$O(n)$	$O(m)$	稳定

1. 算法思路

对于待排序数列，将其元素依次两两进行比较，若第一个元素大于第二个元素，将两个元素进行交换，不断遍历待排序数列并重复比较交换操作直至在一趟序列遍历中没有发生元素交换，完成排序。

2. 算法实现

在经过一次序列遍历后，最后的元素一定是此次遍历序列中最大的数，因此在每次遍历时可以不包含上一次遍历的最后一个元素，去除不必要的以减少程序运行时间。

def bubble_sort(arr):
    arr_len = len(arr)
    if arr_len < 2:
        return
    
    is_sorted = False
    for i in range(1, arr_len):
        if is_sorted:
            return arr
        is_sorted = True
        for j in range(arr_len - i):
            if a[j] > a[j+1]:
                is_sorted = False
                a[j], a[j+1] = a[j+1], a[j]

本博客文章仅供博主学习交流，博主才疏学浅，语言表达能力有限，对知识的理解、编写代码能力都有很多不足，希望各路大神多多包涵，多加指点。