归并排序
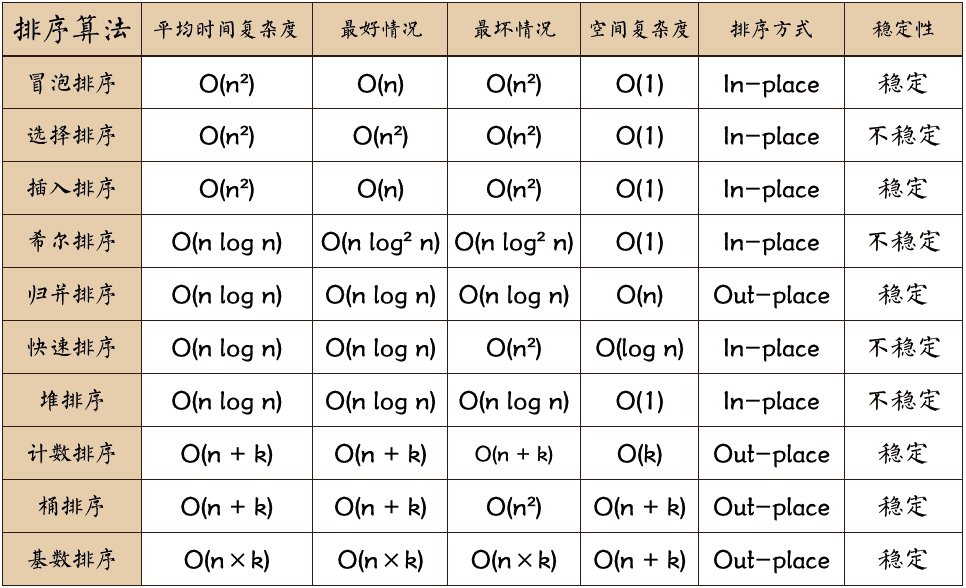
| 排序算法 | 平均时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 冒泡排序 | $O(n^2)$ | $O(1)$ | 稳定 |
| 选择排序 | $O(n^2)$ | $O(1)$ | 不稳定 |
| 插入排序 | $O(n^2)$ | $O(1)$ | 稳定 |
| 希尔排序 | $O(n\log^2 n)$ | $O(1)$ | 不稳定 |
| 归并排序 | $O(n\log^2 n)$ | $O(n)$ | 稳定 |
| 快速排序 | $O(n\log n)$ | $O(\log n)$ | 不稳定 |
| 堆排序 | $O(n\log n)$ | $O(1)$ | 不稳定 |
| 计数排序 | $O(n+k)$ | $O(k)$ | 稳定 |
| 基数排序 | $O(n\times k)$ | 稳定 | |
| 桶排序 | $O(n)$ | $O(m)$ | 稳定 |
算法思路
归并排序遵循分治的思想,将待排序数列分为两个有序子数列,然后合并两个有序子数列为一个完整有序数列,每个子数列也是通过相同的方式变得有序。
算法实现
合并过程:
- 设置指针 index 指向待排序数列的起始位置,设置两个指针 index_l、index_r 分别指向两个子数列的起始位置。
- 比较 index_l、index_r 所指向的元素,将较小的元素写入 index 指针所指的位置,并将 index 指针以及指向较小数列元素的指针后移。
- 重复步骤 2 知道某一子数列指针到达序列末尾。
- 将另一数列剩余元素合并到完整数列末尾。
合并函数:
def merge(arr, start, mid, end):
left, right = arr[start:mid+1], arr[mid+1:end+1]
index, index_l, index_r, len_l, len_r = start, 0, 0, len(left), len(right)
while index_l < len_l and index_r < len_r:
if left[index_l] > right[index_r]:
arr[index] = right[index_r]
index_r += 1
else:
arr[index] = left[index_l]
index_l += 1
index += 1
if index_l < len_l:
arr[index:end+1] = left[index_l:]
if index_r < len_r:
arr[index:end+1] = right[index_r:]
递归版本
def merge_sort_recursion(arr, start, end):
if start >= end:
return
mid = (start + end) // 2
merge_sort_recursion(arr, start, mid)
merge_sort_recursion(arr, mid+1, end)
merge(arr, start, mid, end)
迭代版本
def merge_sort_iter(arr):
arr_len = len(arr)
if arr_len < 2:
return
seq = 1
while seq < arr_len:
i = 0
while i < arr_len - seq:
merge(arr, i, i + seq - 1, min(i + 2 * seq - 1, arr_len - 1))
i += 2 * seq
seq += seq
本博客文章仅供博主学习交流,博主才疏学浅,语言表达能力有限,对知识的理解、编写代码能力都有很多不足,希望各路大神多多包涵,多加指点。